In mechanical design, or structural design, the all most important thing to consider is failure. Rather, how to prevent design failure. As design engineers, we are all too familiar with the stress-strain curve:
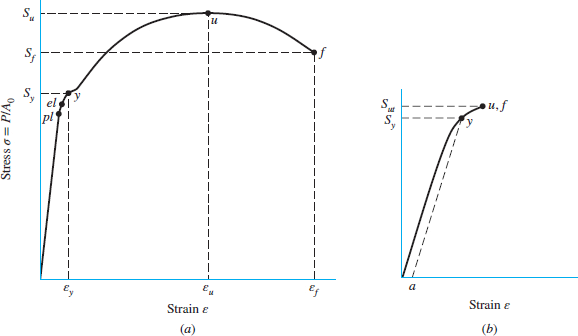
Our eyes automatically go to the ![]() , which represents the yield stress point of the material. That is, the point at which any further stress applied will result in permanent deformation of the material, known as plastic behavior. In theory, the material will not fracture until the fracture point
, which represents the yield stress point of the material. That is, the point at which any further stress applied will result in permanent deformation of the material, known as plastic behavior. In theory, the material will not fracture until the fracture point ![]() is reached; this is the point where the material begins to physically separate.
is reached; this is the point where the material begins to physically separate.
So we could design our components to the ![]() point, right? — Wrong!
point, right? — Wrong!
As engineers, we must always err on the side caution. To remain conservative and safe, we design with the the yield stress ![]() in mind. Why? As always, it helps to study history; back in the 1700s, material testing machines began to make an appearance. With the Industrial Revolution in full force, with the multitude of machines that were being invented and with their high utilization rates, so came the failure of machine elements – phenomena such as distortion, permanent set, cracking, and rupturing were among the component failure modes that engineers were challenged to overcome.
in mind. Why? As always, it helps to study history; back in the 1700s, material testing machines began to make an appearance. With the Industrial Revolution in full force, with the multitude of machines that were being invented and with their high utilization rates, so came the failure of machine elements – phenomena such as distortion, permanent set, cracking, and rupturing were among the component failure modes that engineers were challenged to overcome.
Over the years, hypotheses on failure mechanisms were formulated and tested, leading to today’s failure theories which are now accepted practices. One such theory, is the distortion-energy theory (for ductile materials), which predicts that “yielding occurs when the distortion strain energy per unit volume reaches or exceeds the distortion strain energy per unit volume for yield in simple tension or compression of the same material.” — Whoa! But what does this mean in English?
I.e., the distortion-energy theory says that the culprit behind material failure is distortion of a part, not the volumetric changes in the part. Okay, let’s unpack this. See, when stress is applied to an element, one of two things will happen: 1. It will undergo a change in volume, and/or, 2. it will distort. What’s the difference? First, let’s consider a typical stress element used in describing the state of stress.
Side note: As engineers, it is always important to think from first principles, hence a stress element is about as small as we can take it before entering the atomic world.
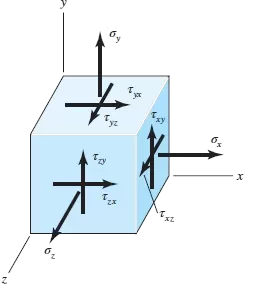
The state of stress at a point (within a structure) may be described by three mutually perpendicular surfaces as shown in the figure above. As the dimensions of the cube approach zero (remember, we’re talking about a point here), the stresses on the hidden faces are equal and opposite, and for the case of equilibrium (![]() ), the cross-shears are equal (
), the cross-shears are equal (![]() , etc.). This results in a total of six stress components to fully define the state of stress for a point,
, etc.). This results in a total of six stress components to fully define the state of stress for a point, ![]() and
and ![]() .
.
Now that we understand what the state of stress of an element looks like, let’s get back to describing the two modes of change due to stress. The figure below shows the original element (left) being equal to a hydrostatic component (center) plus a distortional component (right). Material under stress will undergo one of these two modes of stress or a combination thereof.

To bring distortion-energy theory back down to Earth, I like to refer to the following example. Imagine the rocks below the Earth’s surface (pun intended), pressure is exerted on these rocks mostly uniform in nature (pun) and well beyond their compressive ultimate strengths, yet they don’t fracture! Rocks survive the incredibly large magnitude forces that they are subjected to because their shape is not distorted (as shown in the figure above, right element); i.e., there is no shearing, and therefore there is no failure.
Solving for the distortion energy component ![]() , is done by subtracting the volume change
, is done by subtracting the volume change ![]() from the original element strain energy
from the original element strain energy ![]() , mathematically it is described as follows:
, mathematically it is described as follows:
(1) ![]()
For a simple tension test as shown in the figure below, at yield, ![]() and
and ![]() , and from equation 1, the distortion energy is:
, and from equation 1, the distortion energy is:
(2) ![]()

Therefore, yield is predicted if equation 1 equals or exceeds equation 2, which gives us our third (and final!) equation which happens to define the von Mises stress ![]() :
:
(3) ![]()
Essentially, the von Mises stress ![]() is a single, equivalent, or effective stress for the entire general state of stress for a given element. This is the reason that structural analysis solvers will report von Mises stress (figure below), because the geometry being analyzed is typically so complex, that we as analysts need to quickly refer to a numerical value to grasp the magnitude of the stress across the domain for that mechanical element – the von Mises stress does just that.
is a single, equivalent, or effective stress for the entire general state of stress for a given element. This is the reason that structural analysis solvers will report von Mises stress (figure below), because the geometry being analyzed is typically so complex, that we as analysts need to quickly refer to a numerical value to grasp the magnitude of the stress across the domain for that mechanical element – the von Mises stress does just that.

Equation references: (1, 2, 3).
References
Distortion Energy Theory (http://home.eng.iastate.edu/~gkstarns/me325/lecture21.pdf)
Budynas, R. G., & Nisbett, J. K. (2008). Shigley Mechanical Engineering Design. New York: McGraw-Hill.
Industrial Revolution (https://en.wikipedia.org/wiki/Industrial_Revolution).
Stress tensor (https://slidetodoc.com/finite-element-modeling-and-analysis-ce-595-course/).
Von Mises stress (https://www.youtube.com/watch?v=Smj_F7MN3S4).
